Maximum Likelihood Estimation is Sensitive to Starting Points

In my previous post, I derive a formulation to use maximum likelihood estimation (MLE) in a simple linear regression case. Looking at the formulation for MLE, I had the suspicion that the MLE will be much more sensitive to the starting points of a gradient optimization than other linear regression methods. To demonstrate the sensitivity to the starting points, I ran 10,000 linear regressions. For each starting point I ran a MLE and a root mean square minimization to determine the optimum quadratic parameters to fit a polynomial to the data. As it turns out, the root mean square optimizations were just as good, or better than the MLE for every case. All of the code for this comparison is available here.

Perhaps one of the simplest and most commonly used alternative objective functions for linear regression is the root mean square error (RMSE). RMSE is the square root of the mean square error, and mean square error is the average of the square residuals \( r \). For this purpose, RMSE is defined in the following equation.

The goal of the linear regression would be to find which parameters minimize the RMSE. As it turns out for my particular model and dataset, the optimum of the MLE will be the optimum of minimizing the RMSE. With this in mind I generated 10,000 random starting points. From each starting point I ran a MLE and a minimizing RMSE using gradient optimizations.

It turns out that for the BFGS algorithm, MLE is more sensitive to starting points than minimizing RMSE. I concluded this because of my 10,000 runs the RMSE performed better 7,668 times. Interesting enough the MLE and RMSE were equivalent 2,332 times, and never did the MLE produce a better match than the RMSE method. I’ve included pie chart which helps to visualize the results.

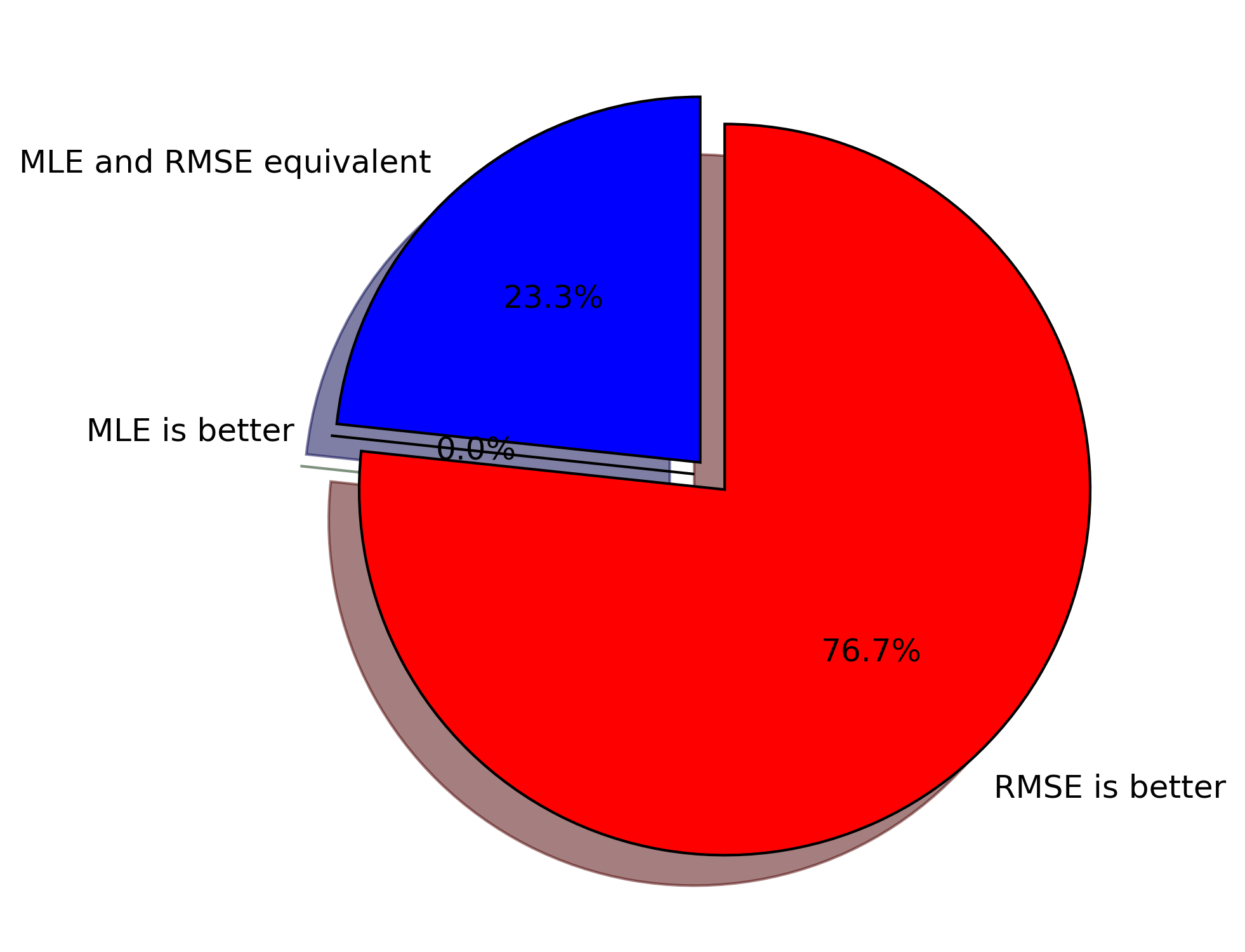
A bit of disclaimer, these results are very model dependent. What happens with my log-likelihood equation is that it has a tendency to go to infinity with a poor starting point, which creates problems with the gradient optimization method.