Comparison of performance: Python NumPy and Numba, MATLAB, and Fortran
September 27, 2017
TL;DR; Python Numba acceleration is really fast.
Like faster than Fortan fast.
Edit February 6, 2018:
Some notes. In Python X += Y; X += Y is faster than X = X + Y + Y which is faster than X = X + 2*Y. However, in MATLAB on my machines X = X + 2*Y is slightly faster than X = X + Y + Y. The Fortran code I run could be marginally improved (<=2% on my machines) by compiling X = X + Y + Y instead of X = X + 2*Y. The code for the Numba, MATLAB, and Fortran benchmark is the same X = X + 2*Y. Benchmarking code is really hard to do, but this quick study was a pleasant introduction to Numba.
Edit September 28, 2017: I’ve updated the benchmark to include runs with gfortran -O2.
Preface
So this post was inspired by a HN comment by CS207 about NumPy performance. The post demonstrates a trick that you can use to increase NumPy’s peformance with integer arrays. Unfortunately the performance gain greatly diminishes when working with double precision floats (though it is still always faster on average). The demo and conversation that follows was interesting, and I got my first taste of Numba (high performance Python acceleration libarary – which has a seamless integration with NumPy).
Introudction
I’m going to benchmark adding big arrays together in NumPy, Numba, MATLAB, and Fortran. It’ll be interesting to see what Numba’s acceleration has to offer since the majoriy of my numerical work is done with NumPy. Many of my colleges still use MATLAB (hopefully my class on Python and this post may convince them to seriously consider Python as an alternative.) Now everyone already knows that Python and MATLAB are slow languages, but NumPy and MATLAB are optimized for array calculations which is what Fortran is all about. And Fortran is fast, so a fair comparison of array operations in Numpy and MATALAB should also consider Fortran.
The Benchmark
The benchmark is going to solve the following equation
where \( X, Y \) are double precision floating point arrays with a lot of elements. I’m going to benchmark this problem for arrays between 1,000,000 and and 1,000,000,000 elements (the most I can fit into my RAM). So essentially I’m going to run functionally equivalent code in Python (either NumPy or NumPy + Numba), MATLAB, and Fortran on two different machines. Machine 1: AMD FX-8370 Eight-Core @ 4.0 GHz with 32 GB DDR3 RAM. Machine 2: ThinkPad 13 i5-6300U with 32 GB DDR4 RAM. I’m not going to touch GPU acceleration in this benchmark, but I think it will be worthwhile to do so sometime.
The benchmark will run \( X = X + 2.0 Y \) 10 times, and return the average run time for 1 dimensional array sizes of 1,000,000, 10,000,000, 100,000,000, and 1,000,000,000 elements. The sample code for one run in each language is provided below.
NumPy code:
import numpy as np
import time as time
n = np.array( int(1e9))# number of data points
X = np.ones(n, dtype=np.float)
Y = np.ones(n, dtype=np.float)
t0 = time.time()
X += Y; X += Y
t1 = time.time()
run_time = t1 - t0
NumPy + Numba single threaded code (inspired by jzwinck):
import numpy as np
import numba
import time as time
@numba.vectorize(["float64(float64,float64)"],
nopython=True,target='cpu')
def add2_par(x, y):
return x + 2 * y
n = np.array( int(1e9))# number of data points
X = np.ones(n, dtype=np.float)
Y = np.ones(n, dtype=np.float)
t0 = time.time()
add2_par(X, Y, out=X)
t1 = time.time()
run_time = t1 - t0
NumPy + Numba parallel code:
import numpy as np
import numba
import time as time
@numba.vectorize(["float64(float64,float64)"],
nopython=True,target='parallel')
def add2_par(x, y):
return x + 2 * y
n = np.array( int(1e9))# number of data points
X = np.ones(n, dtype=np.float)
Y = np.ones(n, dtype=np.float)
t0 = time.time()
add2_par(X, Y, out=X)
t1 = time.time()
run_time = t1 - t0
MATLAB Code:
clear; clc;
% --- single threaded run ---
X = ones(1e9,1);
Y = ones(1e9,1);
t = cputime;
X = X + 2.0*Y;
e = cputime-t;
Fortran code:
program main
c compile with GNU Fortran as
c gfortran -mcmodel=medium demo.f
c
c -mcmodel=medium is only needed for one billion elements
c
c to execture program run ./a.out
implicit none
real*8, dimension(1000000000) :: X
real*8, dimension(1000000000) :: Y
double precision t1, t2
X(:) = 1
Y(:) = 1
call cpu_time ( t1 )
X = X + 2*Y
call cpu_time ( t2 )
write ( *, '(a)' ) 'run time in seconds: '
write ( *, * ) t2-t1
stop
end
Application versions:
| Program | Version |
|---|---|
| Python | 2.7.13 |
| NumPy | 1.13.1 |
| Numba | 0.35.0 |
| MATLAB | R2015a |
| GNU Fortran | 4.8.5 |
Python folder and execution:
> python numpy_bench.py
> python numba_bench_single.py
> python numba_bench_par.py
MATLAB folder and execution:
> matlab -nodesktop -nodisplay -r "run speedTest.m"
Fortran folder and execution:
> gfortran -mcmodel=medium speed1e9.f
> ./a.out
> gfortran speed1e8.f
> ./a.out
> gfortran speed1e7.f
> ./a.out
> gfortran speed1e6.f
> ./a.out
> gfortran -O2 -mcmodel=medium speed1e9.f
> ./a.out
> gfortran -O2 speed1e8.f
> ./a.out
> gfortran -O2 speed1e7.f
> ./a.out
> gfortran -O2 speed1e6.f
> ./a.out
Results
On both of my machines a single threaded Numba run was on average faster than compiled Fortran code (without the -O2 optimization level). With the -O2 optimization level it appears the that Fortan is faster than numba single threaded, but by a very narrow margin. Below you’ll see the mean run times in seconds between gfortran -O2 and the single threaded Python Numba.
| CPU | array elements | gfortran -O2 (s) | Python Numba single (s) |
|---|---|---|---|
| AMD FX-8370 | 1,000,000 | 0.00225 | 0.00202 |
| AMD FX-8370 | 10,000,000 | 0.01952 | 0.01946 |
| AMD FX-8370 | 100,000,000 | 0.19258 | 0.18895 |
| AMD FX-8370 | 1,000,000,000 | 1.90781 | 1.91261 |
| i5-6300u | 1,000,000 | 0.00128 | 0.00098 |
| i5-6300u | 10,000,000 | 0.00996 | 0.01041 |
| i5-6300u | 100,000,000 | 0.10023 | 0.10142 |
| i5-6300u | 1,000,000,000 | 0.94956 | 1.03110 |
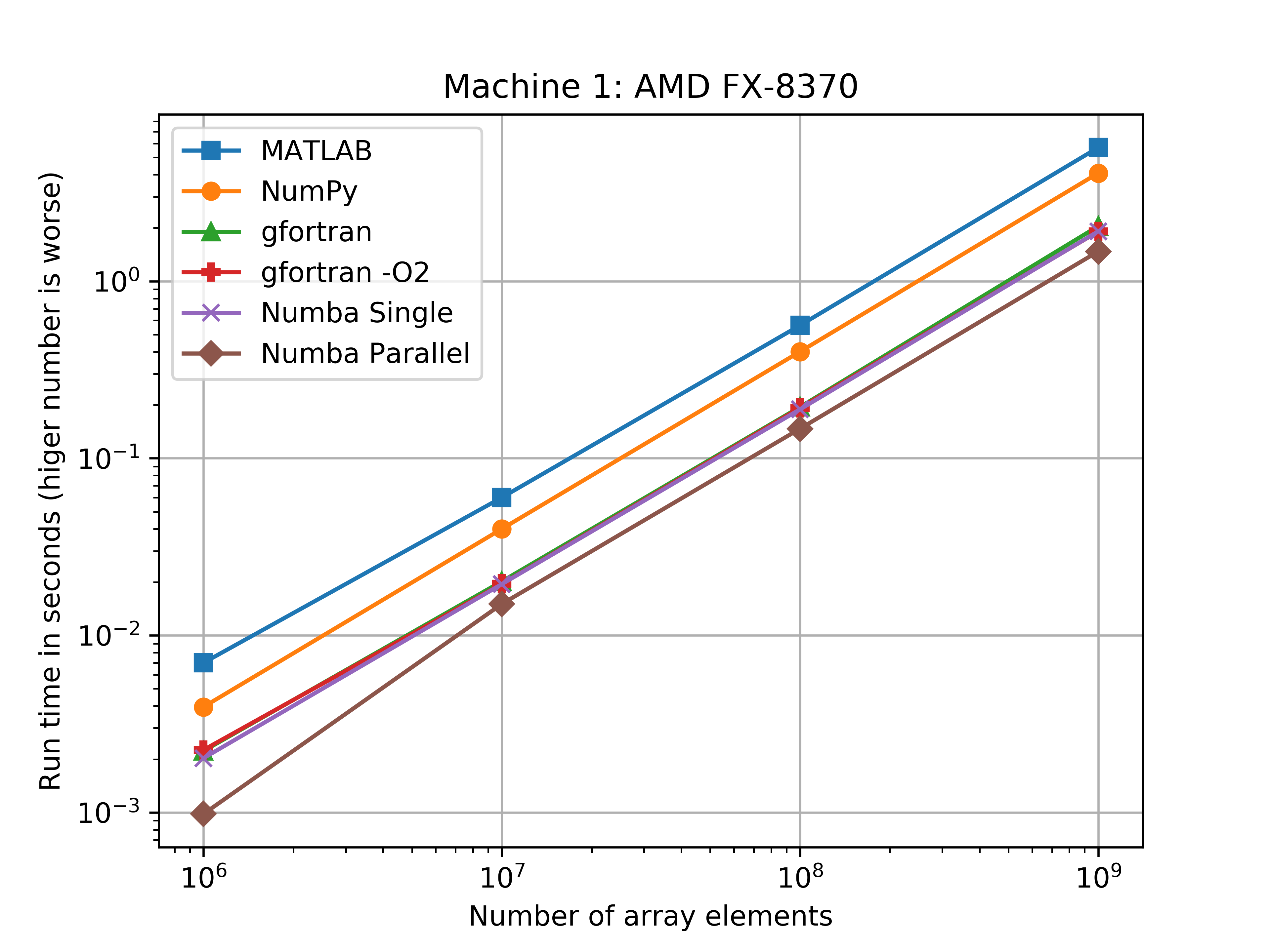
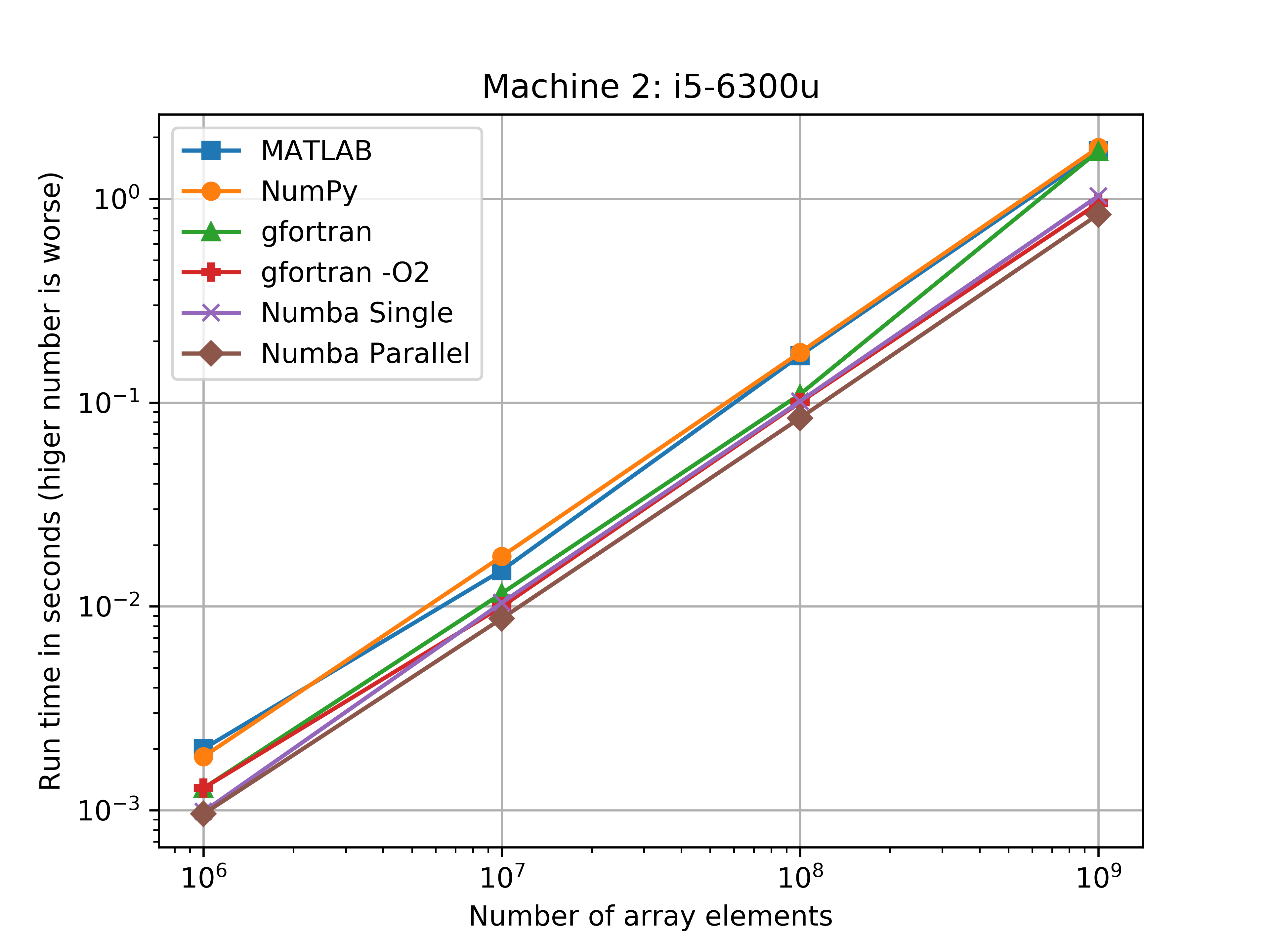
I wasn’t expecting this – and I’m not sure how this black magic called Numba works… I need to do some more research into what Numba is actually doing with the JIT compilation. The speed ranks from Slowest to Fastest on the AMD-FX870: MATLAB, NumPy, gfortran, Numba single thread, gfortran -O2, Numba parallel. With the i5-6300U there is less discrepancy between MATLAB times and NumPy times (they are basically the same).
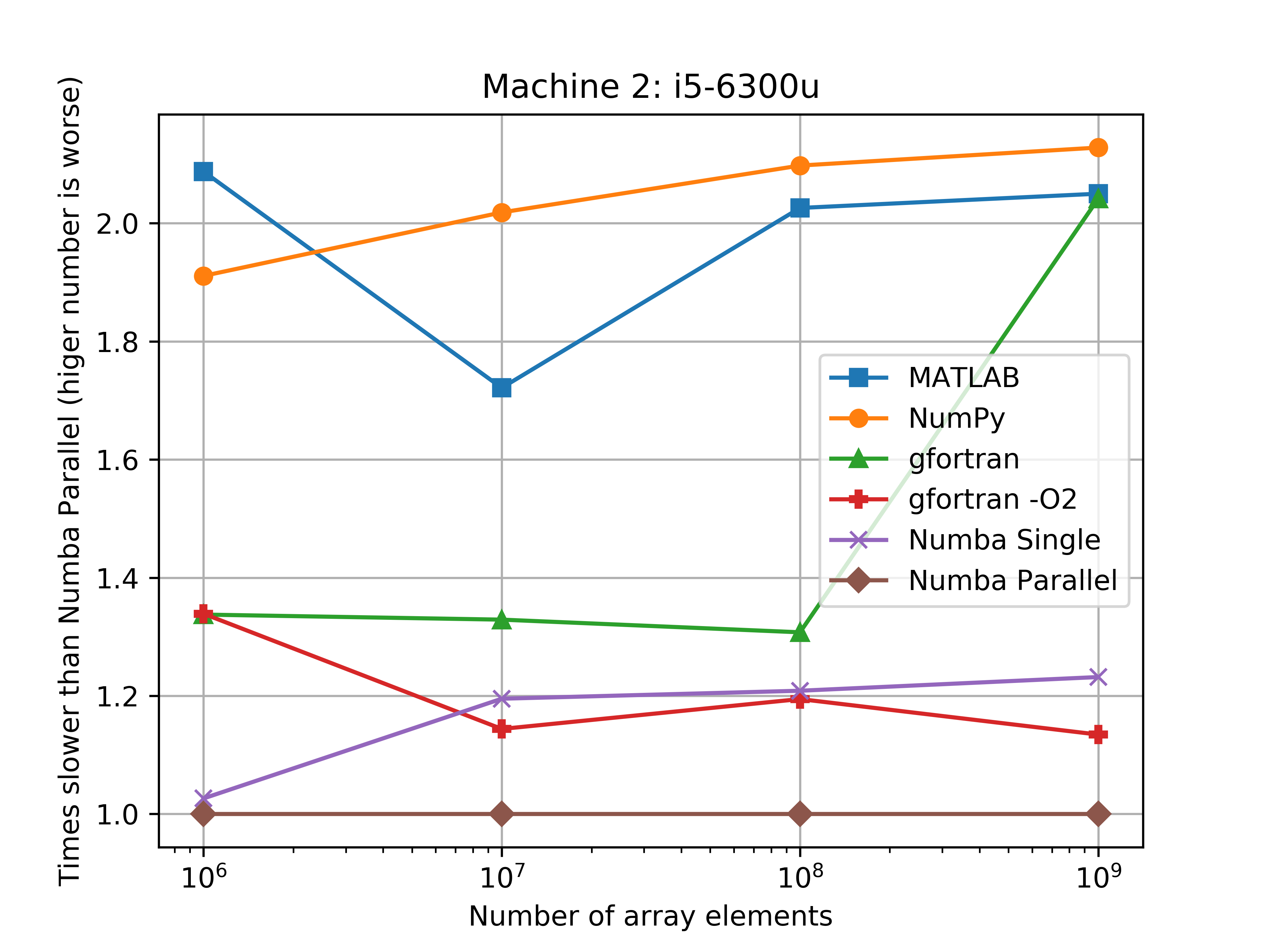
I was also surprised to see with the i5-6300u that NumPy and Fortran ran at nearlly the same speed. For the 1,000,000,000 element arrays, the Fortran code (without the O2 flag) was only 3.7% faster than the NumPy code.
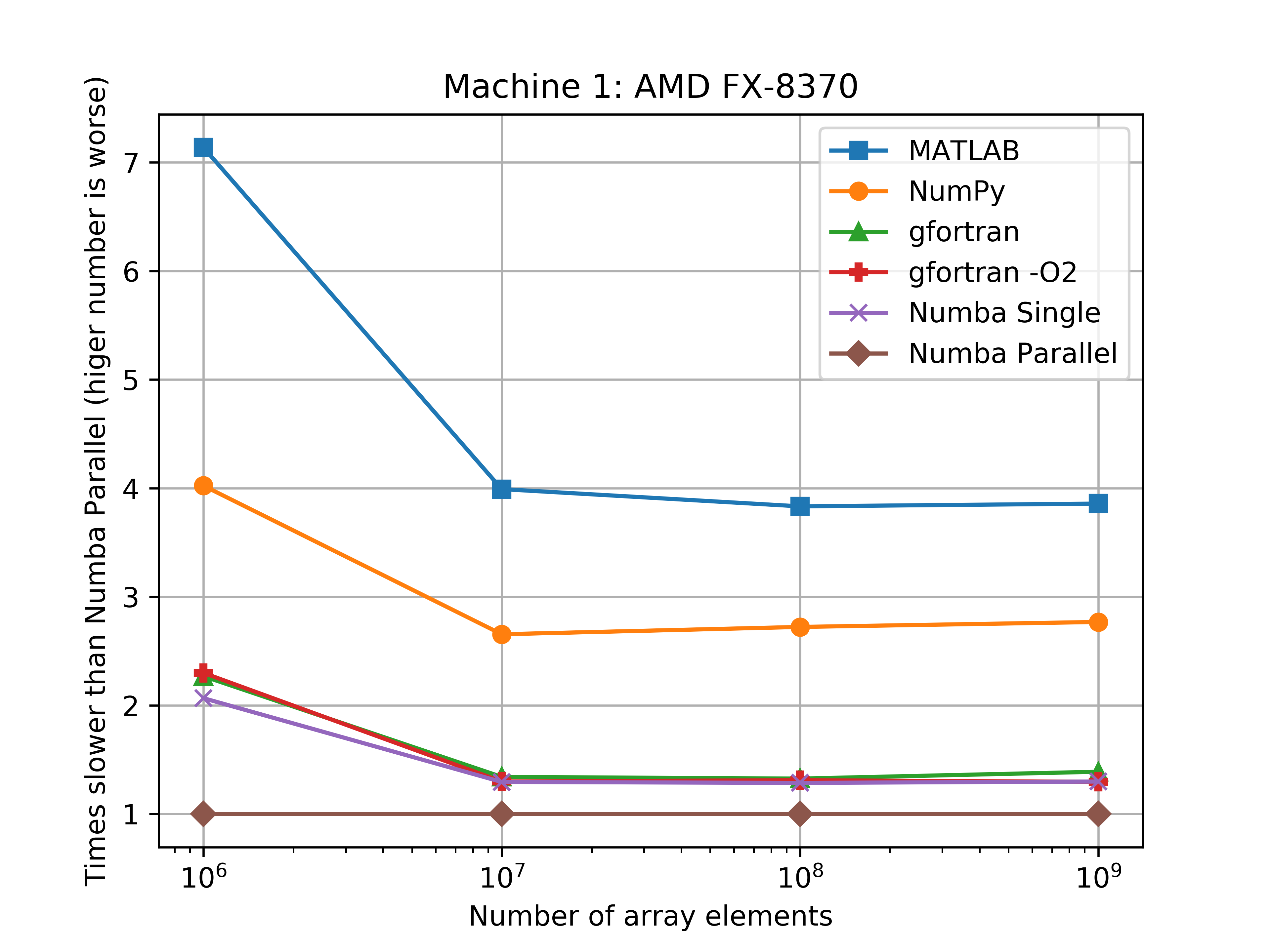
The parallel Numba code really shines with the 8-cores of the AMD-FX870, which was about 4 times faster than MATLAB, and 3 times faster than Numpy. However the parallel Numba code was only about two times faster than Numpy with the i5-6300u, but this makes sences since this is only a two core (4 threads) processor.
The figures bellow show the benchmarks results of the average run times on a log-log scale. Another figure shows how much slower the implementation was when compared to the Numba parallel run average.
Discusion about memory usage
You can’t perform this benchmark without mentioning that this Python example is a Memory HOG wen compared to Fortran and MATLAB. Python will peak at 24 GB of RAM to do the math with the 1,000,000,000 element arrays, regardless of if you use Numba or pure NumPy. This is horribly inefficient – since Python is only storing 16 GB of data in RAM after and before the operation. MATLAB and Fortran solve this problem with a peak memory usage of 16 GB of RAM. This is 33% more RAM required to perform the array operation with Python than MATLAB or Fortran. (Peak RAM usage was estimated using GNU time /usr/bin/time -v)
Conclusion
Wow Numba is Fast. I would have never expected to see a Python NumPy Numba array combination as fast as compiled Fortran code. The cost is obviously that it takes time to port your already existing Python NumPy code to Numba. Numba’s parallel acceleration worked really well on this problem, and with the 8 core AMD-FX870 Numba parallel ran 4 times faster than MATLAB code.
Is there anything I missed? I’m looking forward to playing with Numba GPU acceleration in the future. You can take a look at the code I used to run the benchmark here.
It’s worthwhile to note that I did not do this benchmark with ATLAS, and that using ATLAS may seriously speed up the Fortran execution of this problem (and likely speed up the Numpy and Numba execution as well).