Force piecewise linear fit through data

April 15, 2018

I’ve received a few request for pwlf to perform fits through a particular data point, or set of data points. For instance, you may know that your model must go through the origin (0, 0). We can use Lagrange multipliers to solve a constrained least squares problem to find the best piecewise linear fit while forcing the fit through a set of data points.

Constrained least squares fit

So from my previous post, we have defined a piecewise linear regression problem as

$$ \mathbf{A} \mathbf{\beta} = \mathbf{y} $$

where \(\mathbf{A} \) is our regression matrix, \(\mathbf{\beta} \) is our unknown set of parameters, and \(\mathbf{y} \) is our vector of \(y \) values. We have a set of data points at \((\mathbf{w},\mathbf{z}) \) locations where \( w\) is the \(x \) locations, and \( z\) is the \(y \) locations. We we want to force our fit to go through \((\mathbf{w},\mathbf{z}) \).

I searched for a good explanation of constrained least squares problems, and I think the upcoming book by Boyd and Vandenberghe [1] is great. Essentially we need to construct a constraint matrix \(\mathbf{C} \), such that

$$ \mathbf{C} \mathbf{\beta} = \mathbf{z} $$

is strictly enforced. The constraint matrix \(\mathbf{C} \), is of the exact same form as \(\mathbf{A} \), but evaluated at the \(w \) values as oppose to the \(x \) data points. This means \(\mathbf{C} \) will be a matrix with the number of constraints as rows, and one plus the number of line segments as columns. Using a Lagrangian formulation defined in [1], we can set up the constrained least squares problem as

$$ \begin{bmatrix} 2.0\mathbf{A}^\text{T}\mathbf{A} & \mathbf{C}^\text{T} \\ \mathbf{C} & 0 \\ \end{bmatrix} \begin{bmatrix} \mathbf{\beta} \\ \mathbf{\zeta} \\ \end{bmatrix} = \begin{bmatrix} 2\mathbf{A}^\text{T}\mathbf{y} \\ \mathbf{z} \\ \end{bmatrix} $$

where \(\mathbf{\zeta} \) is some set of Lagrangian multipliers which will be solved along with \(\mathbf{\beta} \). This is the KKT equations for a constrained least squares problem. We are left with a square matrix, which can be used to solve for our unknown set of \(\mathbf{\beta} \) parameters.

Python implementation in pwlf

This has now been implemented into pwlf with the latest version. You can now fit piecewise linear function for a particular number of line segments, and force the fit to go through a particular set of points.

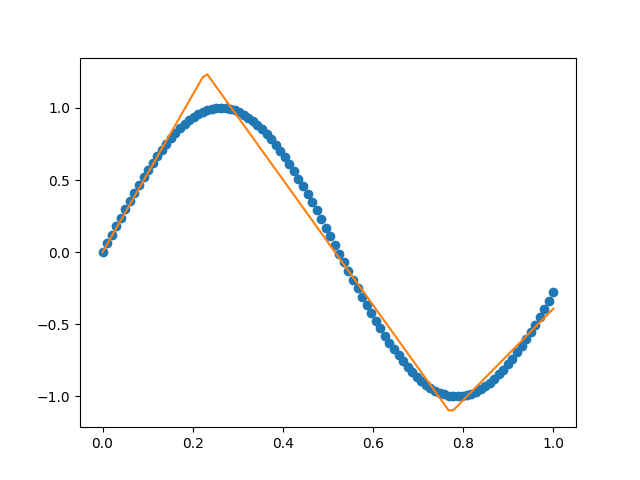
This example shows how you can force a fit through the origin given a set of x y data.


import numpy as np
import pwlf
# Arbitrary sin wave
x = np.linspace(0.0, 1.0, num=100)
y = np.sin(6.0*x)
# initialize pwlf
myPWLF = pwlf.PiecewiseLinFit(x, y, disp_res=True)
x_c = [0.0]
y_c = [0.0]
# fit three line segments, and force fit through (x_c,y_c)
res = myPWLF.fit(3, x_c, y_c)

This will give you a similar fit to the following, which has been forced to go through the origin. PDF of validation accuracy

References

[1] Boyd, Stephen and Vandenberghe, Lieven. Introduction to Applied Linear Algebra - Vectors, Matrices, and Least Squares. Chapter 16 - Constrained least squares. Cambridge University Press. 2018. link

Comments