Compare lstsq performance in Python
April 28, 2019
Edit 2019-05-09: The benchmark has been updated to include the latest CuPy syntax for cupy.linalg.lstsq.
CuPy is a GPU accelerated version of NumPy that is very easy to use. I just submited a PR which adds cupy.linalg.lstsq, and naturally I wanted to compare the least squares performance to numpy.linalg.lstsq. I also compared tensorflow.linalg.lstsq as a reasonable alternative. Hopefully this will provide some insight into when it will pay off to solve least squares problems with CuPy instead of NumPy.
I only have one computer that I was able to run this on so far. I’ll update the post if I can run this benchmark on different hardware.
Least squares solvers
NumPy and CuPy use singular value decomposition (SVD) to solve least squares problems. NumPy defaults to the gelsd lapack routine which is a divide-and-conquer SVD strategy. TensorFlow’s lstsq defaults to using a Cholesky decomposition which should be faster than SVD.
Benchmark
I have a small benchmark problem which performs piecewise linear least squares fits to a sine wave. The benchmark performs fits with known breakpoint locations for 6 and 20 line segments (which translates to solving least squares problem for 6 or 20 unknown parameters). The number of data points was varied from 100 to 6,309,573. This is an odd number, because I couldn’t solve 10**7 data points in the 12 Gb of my GPU’s memory. The code to run the benchmark is available here, and the process to run the code was
python3 sine_benchmark_fixed_six_break_points.py
python3 sine_benchmark_fixed_six_break_points_TFnoGPU.py
python3 sine_benchmark_fixed_twenty_break_points.py
python3 sine_benchmark_fixed_twenty_break_points_TFnoGPU.py
python3 plot_results.py
This code basically runs the following:
import tensorflow as tf
import cupy as cp
import numpy as np
import pwlf
from time import time
import os
n_data = 10**6 # number of data points
np.random.seed(256)
# generate sin wave data
x = np.linspace(0, 10, num=n_data)
y = np.sin(x * np.pi / 2)
# add noise to the data
y = np.random.normal(0, 0.05, size=n_data) + y
my_pwlf = pwlf.PiecewiseLinFit(x, y)
A = my_pwlf.assemble_regression_matrix(breaks, my_pwlf.x_data)
Acp = cp.asarray(A)
ycp = cp.asarray(y)
# numpy.linalg.lstsq
t0 = time()
beta_np, _, _, _ = np.linalg.lstsq(A, y, rcond=1e-15)
t1 = time()
# cupy.linalg.lstsq
t2 = time()
beta_cp = cp.linalg.lstsq(Acp, ycp)
t3 = time()
Atf = tf.convert_to_tensor(A)
ytf = tf.convert_to_tensor(y.reshape(-1, 1))
beta_tf_fast = tf.linalg.lstsq(Atf, ytf, fast=True)
beta_tf_not_fast = tf.linalg.lstsq(Atf, ytf, fast=False)
with tf.Session():
# tf.linalg.lstsq fast=True
t4 = time()
beta_tf = beta_tf_fast.eval()
t5 = time()
I’ve ran the benchmark on the following computers:
| CPU | GPU | OS | TF & NumPy built from source |
|---|---|---|---|
| AMD FX-8350 | NVIDIA TITAN Xp | Linux | Yes |
Results
The results below compare the run time of the fits against the number of data points. The vertical error bars denote the 10th and 90th percentile, considering a Normal distribution with 90% confidence (from the 10 replicate runs).
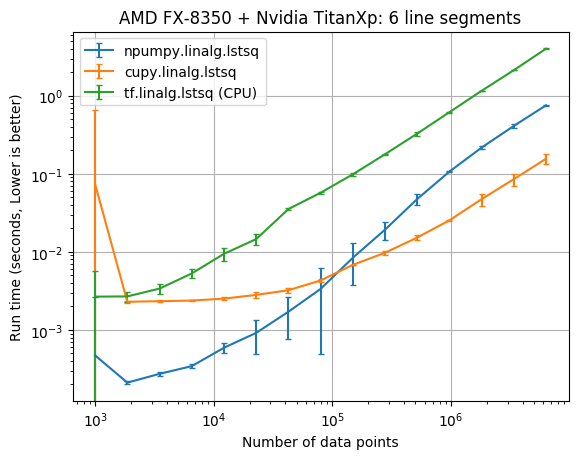
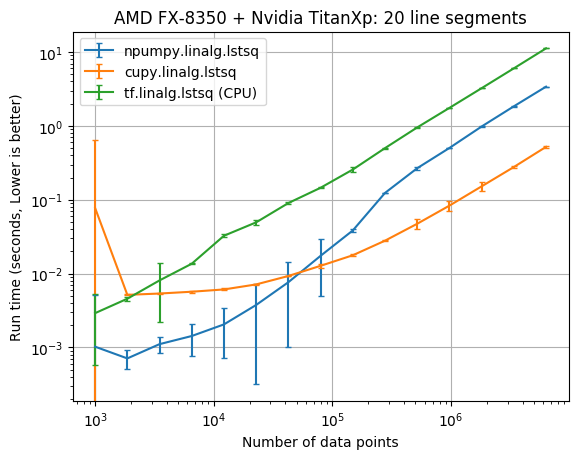
| CPU/GPU | lstsq parameters | Data points | CuPy x faster NumPy |
|---|---|---|---|
| AMD FX-8350/NVIDIA TITAN Xp | 6 | 6,309,573 | 4.84 |
| AMD FX-8350/NVIDIA TITAN Xp | 20 | 6,309,573 | 6.54 |
Disucssion
It appears that the CuPy least squares solver wasn’t faster than NumPy until there was at least 100,000 data points. With 6,309,573 data points cupy.linalg.lstsq was about 6 times faster than numpy.linalg.lstsq.
I should really run this benchmark on a computer with Intel CPU + NVIDIA GPU. Especially since a previous post hinted that TensorFlow performs significantly better on an Intel CPU, and a Cholesky decomposition should be faster than SVD.
NumPy was built from source using Intel MKL on the AMD FX-8350 which isn’t the fastest, however it is the best supported…
Acknowledgements
The TITAN Xp used for this work was donated by the NVIDIA Corporation.